Prima o poi gli studenti di qualsiasi ordine e grado si imbattono nel diagramma di Venn o Eulero Venn. Ma cos’è? Come funziona?
Cominciamo col dire che il diagramma di Venn altro non è che una rappresentazione grafica degli insiemi matematici e non, uno strumento ideato per focalizzare meglio alcuni problemi di insiemistica.
È utile anche in altre discipline, come la linguistica, la logica, la statistica e l’informatica per via dell’immediatezza e dell’intuitività di lettura dei dati.
Due nomi, un unico sistema: Eulero e Venn
Il primo prototipo di rappresentazione grafica degli insiemi venne avanzato nel campo della logica dal matematico svizzero Leonhard Euler, in Italia Eulero, nel 1700.
A lui va il merito dell’elaborazione di quelli che chiamò “cerchi di Eulero”, con cui intendeva chiarire la relazione tra affermazioni, appartenenti a insiemi e sottoinsiemi. La posizione reciproca dei cerchi metteva in evidenza gli elementi comuni e la gerarchia tra insiemi per elaborare nuovi assunti.
Il suo modello venne poi rivisto e completato da John Venn un secolo dopo, utilizzandolo per esplicitare tutte le possibili combinazioni e connessioni tra insiemi.
Cos’è un insieme di elementi?
Reminiscenze dell’epoca delle elementari e medie, ma anche dei primi anni del liceo, riportano alla mente il concetto di insieme, legato al diagramma di Elulero Venn. Senza capire cosa siano gli insiemi non si può utilizzare infatti questo strumento.
Un insieme in matematica è una raccolta di elementi distinti accomunati da una o più caratteristiche, o che appartengono a una stessa lista, a patto che esista un criterio univoco di determinazione per l’inclusione o esclusione dell’elemento stesso dall’insieme. In altre parole, gli elementi di un insieme devono rispettare inequivocabilmente una o più proprietà prestabilite.
Gli insiemi sono solitamente indicati con le lettere maiuscole dell’alfabeto latino, A, B, C, mentre gli elementi contenuti con le lettere minuscole.
Insiemi vuoti, unitari, finiti e infiniti
Il numero degli elementi contenuti in un insieme può essere finito, ad esempio gli studenti della classe 1°B, o infinito, come ad esempio l’insieme dei numeri naturali.
Un insieme finito può contenere anche un solo elemento e in questo caso si chiama insieme unitario.
Infine, un insieme può anche essere vuoto, ossia non contenere nessun elemento.
Appartenenza ed esclusione
Come abbiamo visto un elemento può o meno appartenere a un determinato insieme a seconda del criterio di determinazione. Se un numero, un oggetto, un concetto matematico appartengono all’insieme A, si scriverà che l’elemento a ∈ A, dove la A, ∈ indica proprio “appartiene”. Viceversa, la stessa ∈ barrata vuol dire “non appartiene”.
Le rappresentazioni degli insiemi e il diagramma di Venn
Per rappresentare gli insiemi esistono diverse tipologie di notazioni matematiche. Quella più comune, usata soprattutto quando gli insiemi di cui si parla sono piccoli e contengono pochi elementi, è la rappresentazione tabulare o estensiva o per elencazione, mentre per quelli infiniti si usa la rappresentazione caratteristica o intensiva.
I rudimenti del diagramma di Venn vengono impartiti alla scuola primaria, quando nei primi esercizi di matematica si chiede ai bambini di distinguere elementi uguali in un gruppo variegato: cerchia le pere all’interno del cesto di frutta, individua e raggruppa tutte le vocali dall’insieme delle lettere dell’alfabeto.
Il diagramma di Venn, dal greco “disegno”, sfrutta proprio il cerchio per rappresentare gli insiemi. Gli elementi di un insieme sono raffigurati come punti dispersi in una regione del piano, all’interno di una curva chiusa non intrecciata.
Ogni curva chiusa, o cerchio, rappresenta un insieme diverso ed è individuata da una lettera corrispondente.
Il vantaggio di questa rappresentazione è la grande facilità con cui permette di visualizzare le relazioni tra insiemi tramite la sovrapposizione o meno dei cerchi che li individuano.
Rapporti e combinazioni tra insiemi con il diagramma di Venn
La comprensione delle operazioni tra insiemi, grazie a questo tipo di diagrammi, diventa facile: vediamo l’intersezione, la differenza, l’unione e la complementarietà degli insiemi.
Operazione di intersezione insiemistica
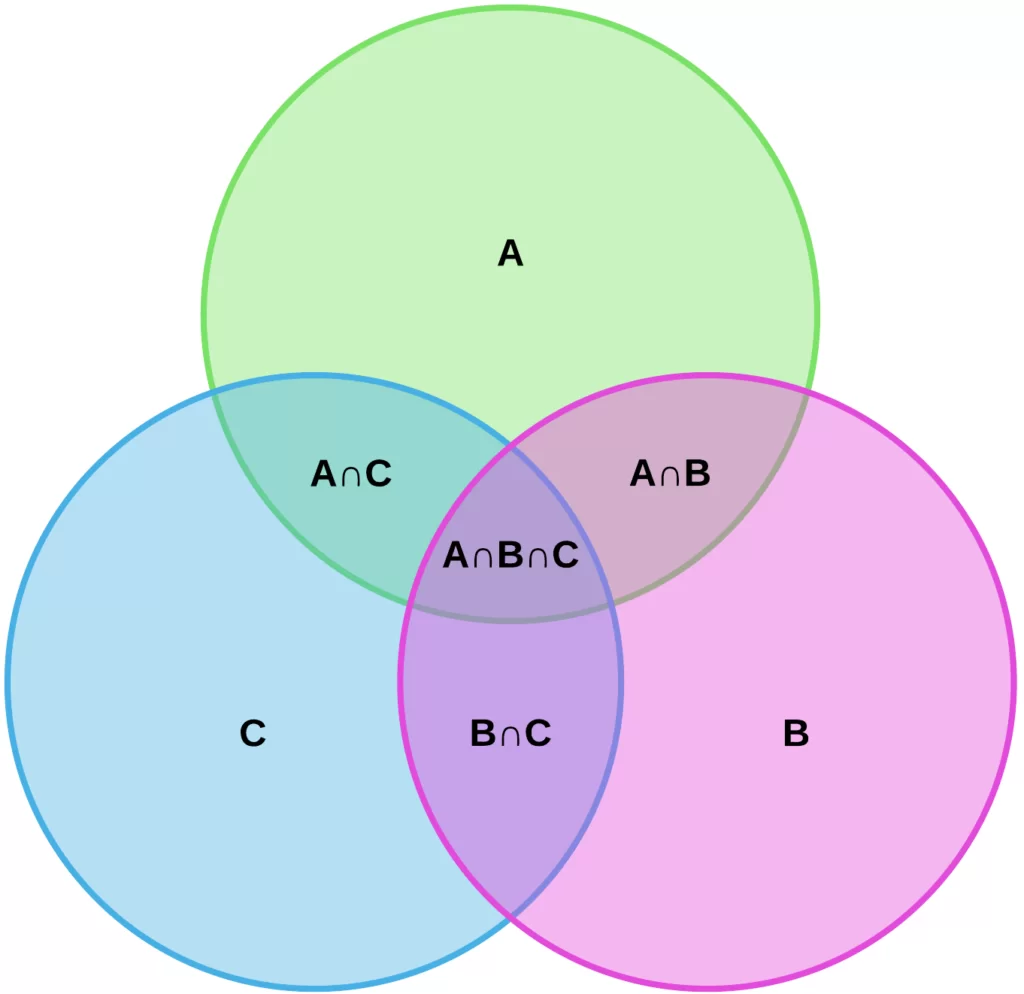
Se due o più insiemi contengono alcuni elementi identici e altri diversi, le curve che li rappresentano si intersecano in una nuova curva chiusa con gli elementi in comune, un nuovo insieme.
Presi quindi due insieme, A e B, la loro intersezione si indica A∩B. A livello grafico avremo due cerchi che si intersecano al centro.
Un esempio pratico potrebbe essere: dati gli insiemi dei numeri A da 1 a 10 e B multipli di 3 compresi tra 1 e 15, troviamo l’insieme intersezione, dove saranno raccolti 3, 6 e 9.
Operazione di differenza insiemistica
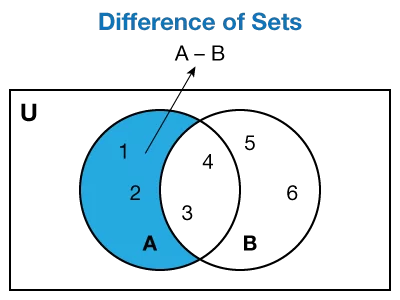
L’insieme differenza contiene tutti gli elementi di un insieme non comuni all’altro insieme. L’ordine in questo caso è fondamentale: A – B e B – A non avranno gli stessi elementi.
Il diagramma di Eulero Venn mette bene in evidenza questa differenza, se colorassamo le porzioni di insiemi non comuni agli altri del caso precedente.
A – B dunque conterrà tutti i numeri da 1 a 10 meno che 3, 6 e 9.
B – A invece sarà composto da 12 e 15.
Operazione di unione insiemistica
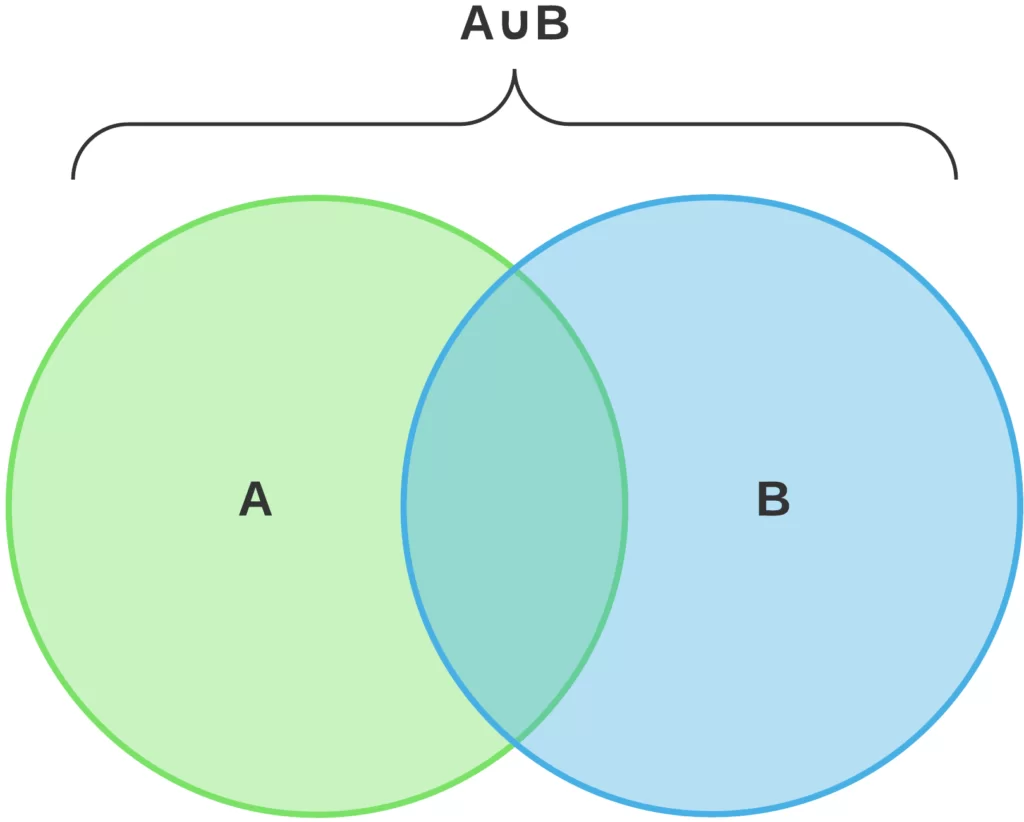
A volte invece è utile sapere quanti sono gli elementi totali di due insiemi, siano essi anche intersecati tra di loro. Si tratterà allora di unione di insiemi, che è in parole povere la “somma” di tutti gli elementi dei due insiemi e si indica con ∩.
Per esempio, presi i due insiemi A={1, 2,4,7,8} e B={4,8,10,12} sarà A∩B={4,8}. Graficamente parlando con i diagrammi di Venn si potrà colorare tutta la porzione interessata dai due insiemi.
Complementarietà insiemistica
Se abbiamo un insieme A, il suo complementare nel cosiddetto insieme ambiente o universo conterrà tutti gli elementi diversi da quelli contenuti in A.
In parole povere, se abbiamo un insieme universo da 10 numeri e l’insieme A composto dai numeri 1 e 2, il suo complementare avrà tutti i numeri fuorché 1 e 2.
Di solito, con la grafica di Venn, si preferisce indicare l’insieme universo con un rettangolo.
I sottoinsiemi nel diagramma di Venn
Come già accennato, i sottoinsiemi come dice il nome sono insiemi contenuti in gruppi più grandi. Significa cioè che tutti gli elementi dell’insieme più piccolo appartengono a un insieme di provenienza.
Se B contiene A si indicherà A⊆B.
Per esempio se B è l’insieme dei numeri da 1 a 10 e A l’insieme dei numeri pari da 1 a 10, è chiaro che A è sottoinsieme di B.
Per disegnarli, basterà tracciare due cerchi concentrici, in cui il più grande ingloba la porzione di piano con gli elementi del più piccolo.
Meno male che c’è internet!
Poiché la matematica e i suoi strumenti risultano spesso ostici ai più, un aiuto può arrivare come sempre dalla rete.
Alcuni siti, infatti, mettono a disposizione degli strumenti per creare e visualizzare meglio il diagramma di Venn online.
Leggi anche: Genitori social, 3 regole per sopravvivere alle chat di classe su WhatsApp



