La studiamo in biologia, la ritroviamo in fisica, ci tartassa in statistica, ma vederla sui libri di scuola e come funziona la distribuzione normale, con la sua bella campana gaussiana, è tutta un’altra cosa dal capirla!
Eppure è uno degli elementi fondanti della matematica moderna, che trova applicazione in una serie di applicazioni nel campo del calcolo degli errori, della fisica, della matematica e del reale.
A cosa serve la distribuzione normale?
In termini matematici, la distribuzione normale è un tipo di distribuzione di probabilità continua usata per descrivere il comportamento di variabili casuali a valori reali che si concentrano intorno a un solo valore medio. Si definisce “normale” perché indica la tendenza delle distribuzioni ad attestarsi con maggiore frequenza intorno a un valore e a discostarsene con minore frequenza.
Come si vede se una distribuzione è normale?
Dati una serie di valori casuali, per capire se siamo al cospetto di una distribuzione normale, rappresentabile tramite la curva di Gauss, bisognerà calcolarne media, mediana e il grado di asimmetria intorno alla media: le prime due devono coincidere mentre la terza non deve superare un determinato valore in funzione della quantità dei dati a disposizione.
Chi inventò la gaussiana?
Johann Friedrich Carl Gauss, matematico e astronomo tedesco, cominciò a usare la sua funzione partendo dall’osservazione dell’orbita del pianeta nano Cerere intorno a Giove. Elaborò quindi il concetto di distribuzione normale standardizzata nel 1828n el suo Theorema egregium dove stabilì gli elementi essenziali che caratterizzavano la sua ben nota campana di Gauss.
Cosa significa gaussiana?
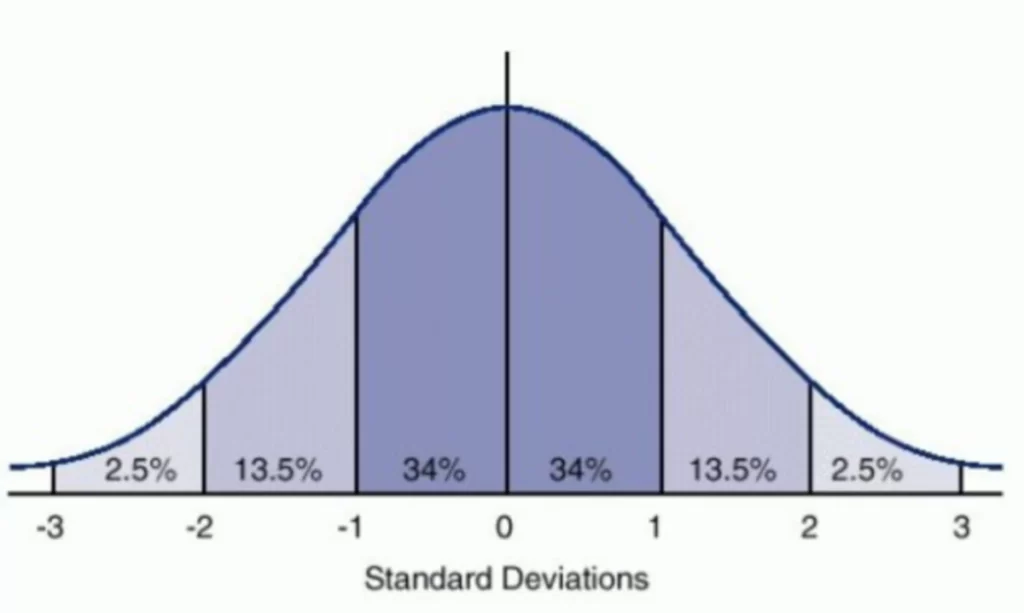
La gaussiana o curva di Gauss è un concetto matematico di geometria differenziale. Essa è definita dalla funzione gaussiana, di formula
Questa funzione viene utilizzata soprattutto in statistica e nella teoria delle probabilità, quando ci si trova davanti a problemi legati alla densità di una distribuzione normale.
Generalmente, nel gergo comune, questo termine è entrato a far parte del registro colloquiale quando si vuol far riferimento a una curva con andamento a campana, dove sono ben evidenti gli estremi laterali rispetto al picco centrale.
Caratteristiche della curva di Gauss
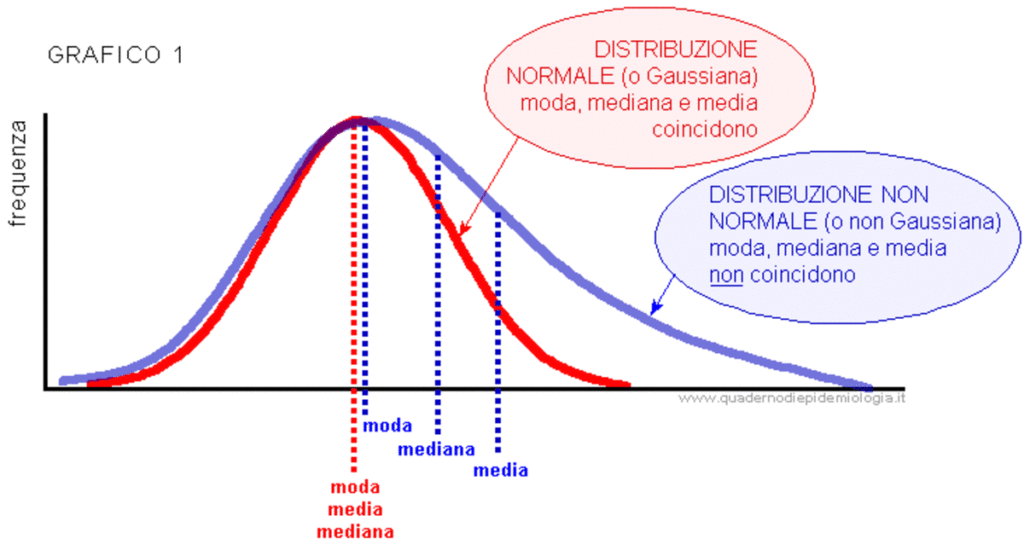
Le gaussiane sono una famiglia di curve che condividono come caratteristica fondamentale il fatto di essere la rappresentazione grafica di un’esponenziale particolare.
Si chiamano code gli estremi della campana, mentre la parte più ampia della curva è detta picco. Più la “vetta” è pronunciata e con maggiore rapidità le code scendono verso lo zero.
Come si dimostra sperimentalmente la curva di Gauss?
Nonostante i principali esperimenti di verifica del teorema di Gauss siano stati condotti nel campo dell’elettromagnetismo, attraverso sofisticati mezzi e calcoli avanzati, una rappresentazione facile e immediata dell’ottenimento della campana si può evincere da una serie di facili passaggi.
Supponiamo di prendere un centinaio di misure della temperatura di una determinata quantità d’acqua su un lasso di tempo determinato.
Al variare del tempo si osserverà che la temperatura subirà un incremento o un decremento riportabile in un grafico XOY con asse delle ascisse in gradi e asse delle ordinate in millisecondi.
Si otterrà un istogramma con un andamento simmetrico a campana in cui è ben evidente la frequenza con cui le singole misurazioni compaiono.
L’asse di simmetria che passa dal vertice della campana corrisponde alla media aritmetica dei dati raccolti.
Come fare una curva gaussiana su Excel?
Seguendo questo procedimento è facile replicare su un fogli Excel per qualsiasi problema di statistica o di distribuzione normale si voglia analizzare.
Ad esempio si possono calcolare le percentuali dei voti ottenuti in un test su tutti gli studenti di un istituto scolastico, la media delle altezze o del peso delle persone di un determinato cluster, gli errori di misurazione effettuati in un laboratorio e così via.
Su Excel bisogna tener conto di tre formule:
- Media aritmetica: si prendono tutti i valori di una colonna A (per esempio) e in una cella diversa C1 si calcola attraverso il comando =MEDIA(A1:A100)
- Deviazione standard: ossia quanto i dati raccolti si discostano dalla media appena ottenuta. In una cella a parte D1 si dovrà digitare =DEV.ST.P(A1:A100)
- Distribuzione normale: infine nella colonna adiacente alle misurazioni si dovrà utilizzare la formula =DISTRIB.NORM(A1;$B$1;$C$1;FALSO)
I dati così ottenuti possono essere messi su un grafico a Dispersione con linee curve che si trova sotto la voce grafici Dispersione nella scheda Inserisci di Excel.
Come si usano le tabelle gaussiane?
Per analizzare la distribuzione normale si un determinato gruppo di valori si ricorre alle tabelle gaussiane che altro non sono che la scrittura matematica della curva di Gauss. Attraverso la lettura delle tabelle sarà possibile individuare con gli opportuni calcoli sia la mediana che il grado di deviazione da questa di tutti i valori riportati. Principalmente vengono utilizzate per i calcoli di stima statistica delle probabilità.
L’esperimento di Galton

Francis Galton ideò un dispositivo, la macchina di Galton, per rappresentare visualmente la distribuzione descritta dalla funzione di Gauss. Su un piano inclinato cosparso da un reticolo ordinato di chiodini si fa scendere una serie di palline che confluiscono in determinati scompartimenti ai piedi del piano dopo aver intrapreso percorsi differenti.
Poiché a ogni incontro con un chiodino ogni pallina può andare a destra o a sinistra con una probabilità del 50%, si noterà che gli scomparti che si riempiono più velocemente e con maggiori quantità di palline sono quelli centrali, mentre quelli esterni saranno raggiunti da un numero assai minore di sferette.
Quali sono le applicazioni nel mondo reale della distribuzione normale?
Innumerevoli sono gli ambiti di applicazione della distribuzione normale, dalla demografia alla medicina, dalla botanica alla genetica, dalla statistica al calcolo delle probabilità, dalla stima dei rischi al meteo.
Ecco una lista di alcuni utilizzi di questo concetto matematico:
- Misura delle caratteristiche genetiche di una popolazione quali altezza, peso e malattie
- Evoluzione
- Calcolo delle probabilità per il lancio dei dadi o della moneta
- Misurazione del livello IQ di un determinato gruppo di persone
- Andamento dei prezzi e dei mercati
- Distribuzione del reddito
- Studio dei fenomeni biologici
Leggi anche: Il diagramma di Venn o di Eulero Venn, applicazioni ed esempi